0. Intro
며칠 전에 풀었던 백준 1504번 문제를 풀 때 사용되었던 다익스트라에 대한 개념을 다시 한번 정리하려고 한다. GeeksforGeeks에서 소개되어 있는 다익스트라 알고리즘 문서를 영문 -> 한국어 번역한 포스트이다. 여기서부터 번역한 내용들이다.
Dijkstra 다익스트라 알고리즘
| 최단 거리 알고리즘, 그리디
그래프와 시작 정점이 주어졌을 때, 시작점부터 주어진 그래프 내의 시작점 제외의 나머지 모든 점들까지의 최단 거리를 찾는 알고리즘이다. 다익스트라 알고리즘은 프림 알고리즘의 MST(최소 스패닝 트리)와 매우 비슷하다. 프림의 MST처럼 시작점을 루트 노드로 하는 SPT(shortest path tree : 최단 거리 트리)가 있다.
두 가지 set이 필요하다.
1: SPT에 포함된 노드들로 이루어진 set2: SPT에 아직 포함되지 않은 노드들로 이루어진 set
알고리즘의 모든 단계에서 2번 set에 있는 노드들 중에서 시작점과 가장 가까이에 있는 점들을 찾는다.
아래는 시작점에서 나머지 모든 점들까지의 최단 거리를 찾기 위한 세부적인 단계들이다.
- 위에서 언급한 1번 set(
sptSet)을 만든다. sptSet은 이미 방문한 정점들로 이루어져 있다. 여기에 포함된 노드들과 - 시작점까지의 최단거리가 이미 계산이 완료된 정점들이다. 빈 set으로 초기화된다. - 주어진 정점들까지의 거리를 할당한다.
distance: 시작점과 정점까지의 거리를 나타내는 변수이다. 처음에는 무한대로 초기화한다. 시작점의 경우는 0으로 초기화한다. 시작점 -> 시작점까지의 거리는 0이니다. 이 시작점부터 먼저 탐색을 시작한다. - While
sptSet이 주어진 모든 정점들을 포함하고 있지 않을 때까지 = 모든 정점들을 방문할 때까지.- sptSet에 아직 포함되지 않은 정점들을 고른다. 그러한 정점들이 여러 개일 경우 가장 짧은 정점을 고른다. 정점
u라고 가정 - 고른 정점
u를 sptSet에 포함한다. = 방문처리 u와 연결되어 있는 정점들까지의 거리를distance업데이트 한다. 단 조건이 있다. 시작점 -u까지의 거리 +u+u와 인접한 정점v까지의 거리가 기존의 시작점 -v까지의 거리보다 작을 경우에만 최단 거리를 갱신한다.
- sptSet에 아직 포함되지 않은 정점들을 고른다. 그러한 정점들이 여러 개일 경우 가장 짧은 정점을 고른다. 정점
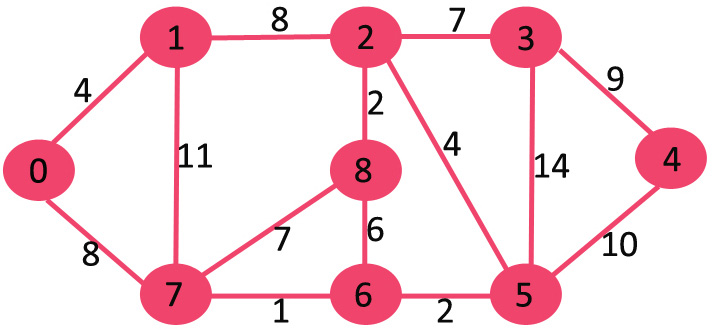주어진 그래프
주요 변수는 2 개이다.
- sptSet : 방문한 정점들을 포함한다.
- distance : 시작점 - 정점까지의 거리를 나타낸다.
sptSet은 처음에는 빈 집합 {}으로 초기화 되고 distance는 {0,INF, INF, INF..}와 같이 시작점은 0으로 나머지는 INF로 초기화된다. 이제 시작점에서 최단 거리인 정점을 고른다. 0번 정점이 선택되고 sptSet에 추가하고 0의 인점 정점들과의 거리를 갱신한다.
- sptSet : {0} 0과 인접한 정점들은 1과 7이다. 현재 distance에는 1과 7모두 처음의 값인 INF가 할당되어 있다. 시작점 - 현재까지의 거리 (0)에서 부터 1과 7까지의 거리를 더한 거리가 INF보다 작을 경우에 distance를 갱신한다.
- 1번 : 0 + 4 < INF
- 7번 : 0 + 8 < INF 두 정점까지의 거리가 모두 INF모다 작으므로 = 더 짧은 거리이므로 거리를 갱신한다.
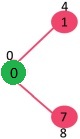방문한 정점(sptSet)은 초록색
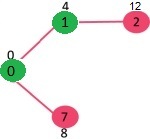
sptSet에 포함되지 않은 정점들 중에 가장 거리가 짧은 인접 정점을 선택한다. 1번 정점이 7번 정점보다 더 짧으므로 (4 < 8)선택되고 sptSet에 추가된다. sptSet : {0,1} 이제 1번과의 인접 노드들의 거리를 갱신한다. 1 -> 2의 거리는 8이고 1번까지의 거리는 이미 4로 갱신되어 있으므로 4 + 8 < IN로 더 짧다. 따라서 2번까지의 거리가 INF에서 12로 갱신된다.
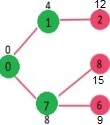
다시, sptSet에 포함되지 않은 정점들 중에 가장 거리가 짧은 인접 정점을 선택한다. 7번 정점이 sptSet에 추가된다. 앞의 단계에서 1번과 7번 중 1번이 더 짧으므로 선택되었으므로 다음으로 짧은 7번이 선택되는 것이다. sptSet : {0, 1, 7} 7번과의 인접 노드들의 거리를 갱신한다. 7번과 인접 정점들은 6과 8 이며 각각 거리가 9, 15로 모두 INF보다 짧다.
다시, sptSet에 포함되지 않은 정점들 중에 가장 거리가 짧은 인접 정점을 선택한다. 6번이 선택된다. sptSet : {0, 1, 7, 6}이 되고 6번과 인접한 정점들까지의 거리를 갱신해준다. 5번과 8번이 갱신된다.
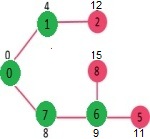
위의 과정들을 sptSet에 모든 정점들이 포함될때까지 반복한다.
- 0과의 거리가 가장 짧은 정점 또는 방문하지 않은 정점을 고른다. = 방문한다.
- 그 점과 인버한 점들과의 거리를 (더 짧다면) 갱신한다. 이 두가지를 계속 반복한다.
모든 정점들이 방문되었고 그 옆의 숫자는 시작점(0)과의 거리를 나타낸다
set이라고 표현했지만 구현은 배열로 했다. 정점 개수 v 길이의 배열을 만들고 각 정점에 해당하는 인덱스의 원소가 true이면 해당 정점은 방문되었다고 = sptSet에 포함된다고 친다. false이면 방문되지 않은 것이다. dist 배열 또한 같은 의미로 정점 = 인덱스로 하여 시작점 - 해당 정점까지의 거리를 나타내는 배열이다.
아래는 GeeksforGeeks에서 제공하는 다익스트라 파이썬 코드이다.
- 정점을 찾고
- 거리를 갱신 하는 과정을 반복하는 와중에 다음 정점을 찾을 때 모든 정점들을 순회하면서 정점을 찾는 부분이 효율적이지 못하다는 약점이 있지만 이후에 heap을 사용하면서 이부분을 줄일 수 있다. 또한 그래프를 2차원 행렬로 표현하고 있다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
# Python program for Dijkstra's single
# source shortest path algorithm. The program is
# for adjacency matrix representation of the graph
# Library for INT_MAX
import sys
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print "Vertex \tDistance from Source"
for node in range(self.V):
print node, "\t", dist[node]
# A utility function to find the vertex with
# minimum distance value, from the set of vertices
# not yet included in shortest path tree
def minDistance(self, dist, sptSet):
# Initialize minimum distance for next node
min = sys.maxint
# Search not nearest vertex not in the
# shortest path tree
for u in range(self.V):
if dist[u] < min and sptSet[u] == False:
min = dist[u]
min_index = u
return min_index
# Function that implements Dijkstra's single source
# shortest path algorithm for a graph represented
# using adjacency matrix representation
def dijkstra(self, src):
dist = [sys.maxint] * self.V
dist[src] = 0
sptSet = [False] * self.V
for cout in range(self.V):
# Pick the minimum distance vertex from
# the set of vertices not yet processed.
# x is always equal to src in first iteration
x = self.minDistance(dist, sptSet)
# Put the minimum distance vertex in the
# shortest path tree
sptSet[x] = True
# Update dist value of the adjacent vertices
# of the picked vertex only if the current
# distance is greater than new distance and
# the vertex in not in the shortest path tree
for y in range(self.V):
if self.graph[x][y] > 0 and sptSet[y] == False and \
dist[y] > dist[x] + self.graph[x][y]:
dist[y] = dist[x] + self.graph[x][y]
self.printSolution(dist)
# Driver program
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]
];
g.dijkstra(0);
# This code is contributed by Divyanshu Mehta
참고
- 위의 코드는 거리만 계산할 뿐 경로에 대한 정보는 계산하지 않는다. 또 하나의 배열을 추가해서 경로를 저장하고 갱신하는 과정을 추가할 수 있다. 따라서 시작점부터의 모든 정점들의 순서를 알 수 있다.
- 위의 코드는 무방향 그래프를 가정하고 있다.
- 하나의 정점 -> 여러 개의 도착점까지의 최단 거리를 구하고 있다. 그러나 하나의 도착점까지의 거리만을 구하고 싶다면 for문에서 중간에 break할 수도 있다.
- 시간 복잡도는
V^2이다. 만약 주어진 그래프가 인접리스트로 표현되었다면E Log V로 줄일 수 있다. - 다익스트라 알고리즘은 음의 가중치를 가진 그래프에는 적용되지 않는다. 하나의 정점을 여러 번 방문하는 방식으로 정답을 도출할 수도 있겠지만 그만큼 시간 복잡도가 나빠진다. 음의 가중치가 있을 경우 벨만-포드 알고리즘을 사용한다.
다음 포스트
- Dijkstra’s Algorithm for Adjacency List Representation : 인접 리스트로 표현된 다익스트라 알고리즘
- Printing Paths in Dijkstra’s Shortest Path Algorithm : 다익스트라에서 경로(정점들의 순서)를 출력하기